Un arbre triplet forme l’une des structures les plus belles en mathématiques
Les nombres de Markov révèlent les secrets des nombres irrationnels et les motifs de la suite de Fibonacci. Cependant, il y a une question à leur sujet qui résiste à la démonstration depuis plus d’un siècle
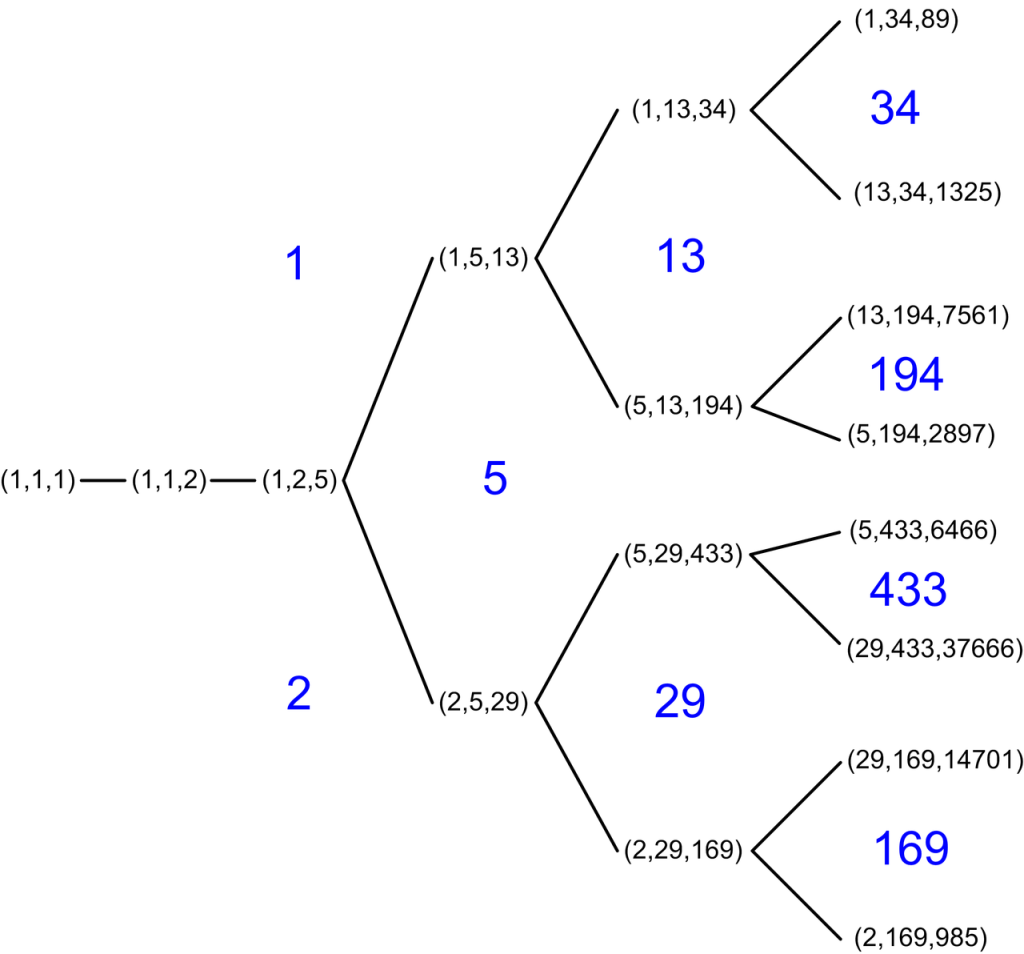
Cet arbre montre comment vous pouvez déterminer de manière unique un triplet de Markov. Commencez par le plus grand nombre de votre triplet. Ensuite, croisez deux branches adjacentes pour descendre dans l’arbre. Par exemple, si vous commencez par 194, vous atteindrez 13 et 5.
La plupart des gens connaissent seulement quelques nombres qui ne peuvent pas être écrits comme des fractions, comme √2 ou π. Mais de tels nombres, appelés nombres irrationnels, sont bien plus nombreux que les fractions ou les nombres rationnels.
À quel point sont-ils faciles à approximer avec des fractions ? Si vous utilisez une fraction avec un dénominateur arbitrairement grand, vous pouvez vous rapprocher arbitrairement. (Comme on le sait bien, 22/7 donne une bonne approximation de π ; 355/113 est encore meilleure.) Mais certains nombres irrationnels sont plus difficiles à approximer que d’autres, ce qui signifie que vous devez utiliser un dénominateur très grand pour obtenir une approximation proche. Le plus difficile s’avère être le nombre d’or, ϕ, ou (1+√5)/2. Il est, dans un sens mathématique spécifique, le nombre qui est le plus “éloigné” d’être rationnel.
Quel est le suivant le plus éloigné ? Et le suivant ? La séquence des nombres irrationnels difficiles à approximer s’avère être donnée par les solutions entières à une équation qui semble simple mais qui n’a pas de lien évident avec l’approximation des nombres irrationnels. Ce lien a été prouvé par Andrey Markov, un mathématicien russe perspicace, en 1879.
Markov est célèbre pour avoir proposé un concept en théorie des probabilités appelé chaînes de Markov, qui sont utilisées dans tout, de l’algorithme PageRank de Google aux modèles d’évolution de l’ADN. Bien que les solutions à son équation, appelées nombres de Markov, ne soient pas aussi connues, elles apparaissent dans une vaste gamme de disciplines mathématiques, notamment la combinatoire, la théorie des nombres, la géométrie et la théorie des graphes.
“C’est non seulement une équation, c’est une sorte de méthode”, a déclaré Oleg Karpenkov, mathématicien à l’Université de Liverpool. “Ces nombres sont au cœur, profondément ancrés dans les mathématiques… des structures comme celle-ci sont le genre d’idées rares.”
Son équation, x2+y2+z2=3xyz, a une solution entière évidente lorsque x, y et z sont tous égaux à 1 (puisque 1 + 1 + 1 = 3 × 1). Il s’avère que toutes les solutions entières de l’équation sont reliées par une règle simple. Commencez par une solution (a, b, c). Ensuite, le triplet lié (a, b, 3ab − c) est également une solution. Les deux premiers nombres restent les mêmes, tandis que c, le troisième, est remplacé par 3ab − c. Appliquez cette règle à (1, 1, 1) et vous obtiendrez (1, 1, 2). (Il est facile de vérifier que l’insertion de ces valeurs rend les deux côtés de l’équation égaux à 6.) Appliquez à nouveau la règle, et vous reviendrez là où vous avez commencé, puisque 3 − 2 = 1. Mais si vous inversez l’ordre des nombres dans le triplet avant d’appliquer la règle, cela crée tout un univers de solutions. Si vous entrez (1, 2, 1), vous obtiendrez (1, 2, 5).
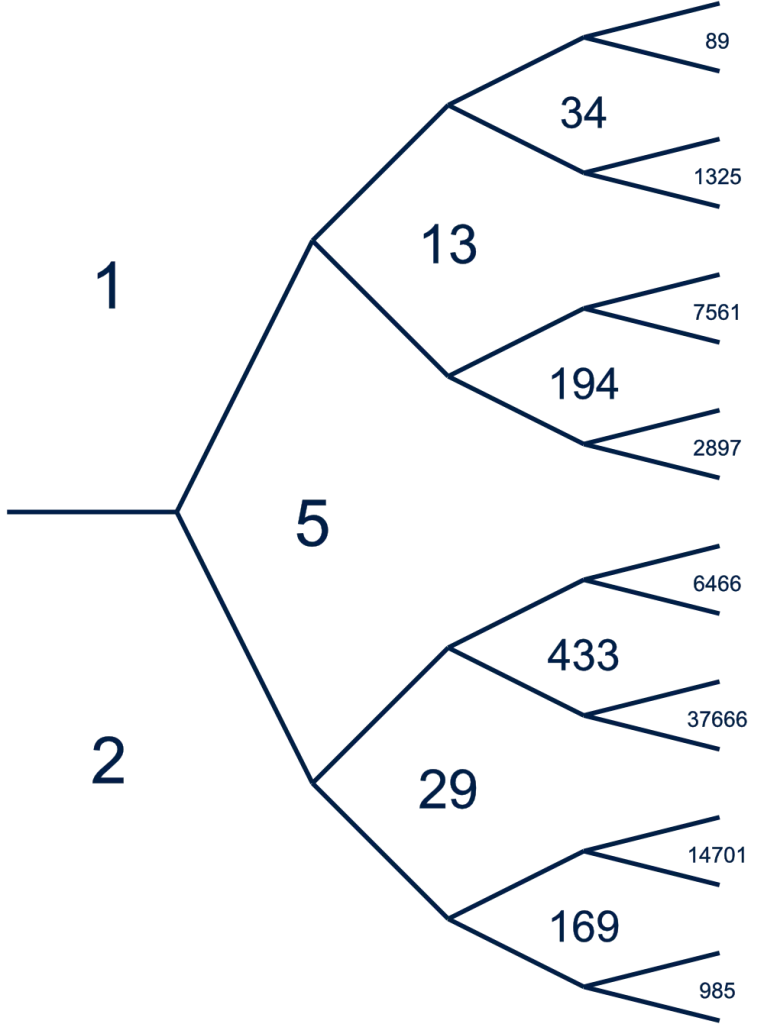
La suite de Nombres de Markov occupent une place centrale, profonde à l’intérieur des mathématiques… des structures comme celle-ci sont le genre d’idées rares.
Jusqu’à présent, en raison des 1 identiques, l’arbre (illustré au début de cette histoire) ne se ramifie pas — les premières étapes font pousser le tronc de l’arbre, pour ainsi dire. Mais si vous commencez avec une solution ayant trois nombres différents, comme (1, 2, 5), les branches commencent à proliférer. Entrez (5, 1, 2) et vous obtenez (2, 5, 29). Mais (2, 5, 1) donne (1, 5, 13). (Si vous entrez (1,2,5), alors la règle vous ramène à une branche inférieure de l’arbre.) À partir de ce point, chaque solution a trois nombres différents, de sorte que chaque branche de l’arbre mène à deux nouvelles branches.
La branche la plus à gauche de l’arbre peut sembler familière — elle contient tous les autres nombres de la suite de Fibonacci, l’une des plus connues en mathématiques (chaque nombre de cette suite est la somme des deux termes précédents : 1, 1, 2, 3, 5, 8, 13, 21, 34, …). La branche la plus à droite contient de manière similaire chaque autre terme de la suite de Pell, une suite liée, quoique légèrement moins célèbre. La façon dont ces suites apparaissent dans l’arbre des solutions est “l’une des choses les plus belles en mathématiques que je connaisse”, a déclaré Alexander Gamburd, professeur à la City University de New York.
Le théorème de Markov de 1879, reliant chaque triplet à un nombre irrationnel difficile à approximer, était le premier indice que cette équation pourrait résonner profondément dans les mathématiques. Dans un livre de 2013 sur le sujet, Martin Aigner, un mathématicien autrichien décédé en octobre, a appelé le théorème “sans aucun doute l’un des classiques de tous les temps en théorie des nombres”.
En 1913, Georg Frobenius, un mathématicien allemand qui a apporté des contributions importantes à l’algèbre, la théorie des nombres et l’étude des équations différentielles, a remarqué quelque chose de curieux à propos des triplets de Markov. Chaque plus grand nombre semblait déterminer de manière unique les deux plus petits. Un nombre — prenons 5 par exemple — pourrait apparaître dans de nombreux triplets, tels que (1, 2, 5), (1, 5, 13), (2, 5, 29), et ainsi de suite. Mais, a-t-il observé, si l’on examine uniquement le plus grand nombre de chaque triplet, il sera affilié à seulement une paire de nombres plus petits.
La simplicité relative de la conjecture illustre un paradoxe mathématique courant. Des outils tels que l’équation de Markov peuvent être utilisés pour prouver des résultats subtils et complexes même lorsque des questions de base sur leurs propriétés restent non résolues.
Cependant, ces dernières années, des progrès notables ont été réalisés vers la démonstration de la conjecture d’unicité. On sait depuis longtemps qu’il est possible d’établir une correspondance entre chaque triplet de Markov et toutes les fractions entre zéro et 1. Pour chaque fraction p/q, appelée indice, vous pouvez attribuer un nombre de Markov mp/q en suivant une procédure mathématique particulière. Par exemple, m2/3 est 29, et m3/5 est 433.
En 2013, Aigner a formulé trois conjectures sur la manière dont les triplets peuvent être ordonnés en utilisant cette correspondance. Ces conjectures sont des étapes vers la démonstration de la conjecture d’unicité. Il a émis l’hypothèse que si vous gardez le numérateur de l’indice constant et augmentez le dénominateur (comme dans 1/2, 1/3, 1/4, 1/5, …), les nombres de Markov respectifs continueront d’augmenter. De même, il pensait que si vous augmentez le numérateur mais gardez le même dénominateur (comme dans 1/17, 2/17, 3/17, 4/17, …), vous devriez également obtenir une série de nombres de Markov de plus en plus grands. Le même schéma de nombres croissants, pensait-il, devrait se maintenir si la somme du numérateur et du dénominateur est maintenue constante (comme dans 1/100, 2/99, 3/98, …).
La conjecture du numérateur constant a été démontrée dans un article de 2020 dans Advances in Mathematics par Michelle Rabideau de l’Université de Hartford et Ralf Schiffler de l’Université du Connecticut. En février 2023, avec deux autres collaborateurs, Rabideau et Schiffler ont publié une démonstration des deux autres conjectures également.
En raison de ces avancées et d’autres encore, Karpenkov est optimiste quant à la possibilité qu’une démonstration de la conjecture d’unicité de Frobenius soit enfin en préparation. “Je connais des gens qui disent qu’ils sont près de le prouver”, a-t-il déclaré. “Je pense que nous sommes assez proches, peut-être dans les cinq prochaines années.”
